Curie temperature
The Curie temperature (Tc), or Curie point, is a term in physics and materials science, named after Pierre Curie (1859–1906), and refers to a characteristic property of a ferromagnetic or piezoelectric material.
Contents |
Curie temperature in ferromagnetic and ferrimagnetic materials
The Curie temperature of a ferromagnetic or a ferrimagnetic material is the reversible point above which it becomes paramagnetic. Given below are various Curie temperatures for different substances.[1]
| Substance | Curie temp °C |
|---|---|
| Iron (Fe) | 770 |
| Cobalt (Co) | 1130 |
| Nickel (Ni) | 358 |
| Iron Oxide (Fe2O3) | 622 |
Below the Curie temperature the magnetic moments are aligned parallel within magnetic domains in ferromagnetic materials and anti-parallel in antiferrimagnetic materials. As the temperature is increased towards the Curie point, the alignment (magnetization) within each domain decreases. Above the Curie temperature, the material is paramagnetic so that magnetic moments are in a completely disordered state.
The destruction of magnetization at the Curie temperature is a second-order phase transition and a critical point where the magnetic susceptibility is theoretically infinite.
A heat-induced ferromagnetic-paramagnetic transition is used in magneto-optical storage media, where it is used for erasing and writing of new data. Famous examples include the Sony Minidisc format, as well as the now-obsolete CD-MO format.
Other uses include temperature control in soldering irons such as those made by Metcal and the Weller WTCPT and, in general, where a temperature-controlled magnetization is desirable.
Curie temperature in piezoelectric material
In analogy to ferromagnetic materials, the Curie temperature is also used in piezoelectric materials to describe the temperature above which the material loses its spontaneous polarization and piezoelectric characteristics. In lead zirconate titanate (PZT), the material is tetragonal below Tc and the unit cell contains a displaced central cation and hence a net dipole moment. Above Tc, the material is cubic and the central cation is no longer displaced from the centre of the unit cell. Hence, there is no net dipole moment and no spontaneous polarization.
Curie-Weiss law 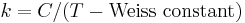
See also
- See ferromagnetism for a list of ferromagnetic materials and their Curie temperatures.
- Ferroelectric effect
- Néel temperature
- Pierre Curie
References
- ↑ Buschow, K. H. J.Encyclopedia of materials : science and technology, Elsevier, 2001 ISBN 0-08-043152-6 page 5021 table 1
Introduction to Solid State Physics 7th ed. (1996) by Charles Kittel
External links
- Ferromagnetic Curie Point. Video by Walter Lewin, M.I.T.